সংখ্যার সাধারণ নিয়মগুলি অনেক আশ্চর্যজনক প্রভাব তৈরি করে। এখানে তিনটি গণিতের কৌশল বা ট্রিক্স আছে, যা বন্ধুদের সামনে আপনাকে বুদ্ধিমান প্রমান করতে সাহায্য করবে সহজেই। প্রথমে কৌশলগুলো ভালো করে পড়ে নিন এবং আপনার বন্ধুদের গণিত দক্ষতার সাথে মেলে এমন কৌশলটি নির্বাচন করুন।
#1 কৌশল ১- একটি নাম্বার মনে মনে কল্পনা করা (সহজ)
১ আপনার বন্ধুকে মনে মনে একটি নম্বর বাছাই করতে বলুন। নাম্বারটি আপনাকে বলতে মানা করুন এবং মনে রাখতে বলুন শেষ পর্যন্ত।
আমরা একটি উদাহরণে যাব যেখানে আপনার বন্ধুটি ৬ নম্বরটি তুলবে।
এমনকি বাচ্চারাও এই কৌশলটিতে গণিতটি করতে পারবে, কেনোনা এখানে কেবল ২ দিয়ে গুণ এবং ভাগ করতে হবে। তবে বেশি ছোট বাচ্চাদের ক্ষেত্রে অন্য কাউকে কানে কানে বলে রাখতে পারে মনে রাখার সুবিধার জন্য।
#2
#3
#4
#5
#6
উত্তরটি ঘোষণা করুন আসুন দেখি কেন এটি কাজ করে। ৫. আপনার বন্ধুটি যে সংখ্যাটি বেছে নিয়েছে তা বিবেচনা না করেই তার চূড়ান্ত উত্তর হিসাবে তিনি ৫ টি দিয়ে শেষ করবেন।
ঘোষণা করুন যে আপনি তাঁর মন পড়েছেন, এবং আপনার বন্ধুটি লিখেছেন সর্বশেষ নম্বরটি ৫। যদি ঘরে অন্য কোনও লোক থাকে, আপনার বন্ধুটিকে প্রমাণ করার জন্য তাদের কাগজের টুকরোটি দেখিয়ে দিন।
Leave a Reply
GIPHY App Key not set. Please check settings
#7
কৌশল ২ ট্রিক ৩৭ (কিছুটা কঠিন)
বেশিরভাগ ধাপই এখানে কেবল সমস্যাটিকে আপনার বন্ধুর পক্ষে ধরতে পারা জটিল করতে করা হয়েছে। আপনি নির্বাচিত সংখ্যা দ্বিগুণ করার পরে, এটিকে ২ দ্বারা ভাগ করলেন এবং সংখ্যাটি বিয়োগ করলেন, আপনি মূলত আসল সংখ্যাটিই সম্পূর্ণ বাতিল করে দিয়েছেন।
এখন আপনার বন্ধুটি কী পছন্দ করেছে তা বিবেচ্য নয়। উত্তরটি কেবলমাত্র তাঁকে অতিরিক্ত যে সংখ্যা এবং নির্দেশনা দিয়েছিলেন তার উপর নির্ভর করে যা এই কৌশলটিতে ৫ এর দিকে পরিচালিত করে।
Leave a Reply
GIPHY App Key not set. Please check settings
#8
১ একজনকে ৩ বার একই অঙ্ক লিখতে বলুন। অবশ্যই সে আপনার কাছে কাগজটি সর্বদা লুকিয়ে রাখবে। একটি ক্যালকুলেটর এখানে কাজে আসবে।
উদাহরণস্বরূপ, তিনি ৫৫৫ লিখে রাখতে পারেন।
২ তিনটি সংখ্যাকে একসাথে যোগ করার নির্দেশ দিন। আপনি যার মন পড়তে চেষ্টা করছেন তাকে তিনটি সংখ্যা আলাদা করতে এবং তাদের একসাথে যোগ করতে বলুন।
এই উদাহরণে, ৫+৫+৫ = ১৫।
Leave a Reply
GIPHY App Key not set. Please check settings
#9
৩ বড় সংখ্যাটিকে ছোটটি দিয়ে ভাগ করুন। নিশ্চিত করুন যে, তার কাছে এখন দুটি সংখ্যা লিখিত আছে, একটি তিন-অঙ্কের নম্বর এবং আর অন্যটি এর চেয়ে ছোট একটি সংখ্যা। তাকে তিন অঙ্কের সংখ্যাটি নিয়ে এবং এর চেয়ে ছোটটি দিয়ে ভাগ করতে বলুন।
৫৫৫÷ ১৫ = ৩৭।
Leave a Reply
GIPHY App Key not set. Please check settings
#10
#11
৫ আসুন জেনে নিই কেন এটি কাজ করে। এখানে কোন কঠিন কৌশল নেই; এগুলি কেবল সংখ্যার নিজস্ব বৈশিষ্ট্য। ৩৭ x ৩ = ১১১. প্রতিবার আরও 111 যোগ করে(১১১ → ২২২ → ৩৩৩, ইত্যাদি), তাই আপনি প্রতিবার তিনটি অংক দ্বারা 37 গুণক যোগ করছেন। সংখ্যার যোগফল (১ ১ ১ → ২ ২ ২ → ৩ ৩ ৩ ইত্যাদি) এর দিকে তাকালেও আপনি দেখবেন যে প্রতিবার তিনটি যুক্ত হচ্ছে। যাকে একটি বিভাজ্য সমস্যার মধ্যে রাখা হলে, প্রতিবার সংখ্যাটি কে আরও তিন দিয়ে ভাগ করা হলো। যা একে অপরকে বাতিল করে দেয় এবং আপনি ৩৭ এই ফিরে আসবেন।
Leave a Reply
GIPHY App Key not set. Please check settings
#12
১ যার মন পড়তে চাচ্ছেন তার হাতে একটি ক্যালকুলেটর, পেন্সিল এবং কাগজ দিন। এই কৌশলটিতে বড় বড় সংখ্যা আসবে, তাই প্রচুর জায়গা আছে এমন ক্যালকুলেটর নির্বাচন করুন।
বলুন যে আপনি তাঁর মন পড়ছেন, এবং সে যেনো কাগজ এবং ক্যালকুলেটরের সমস্ত কিছুই আপনার কাছ থেকে গোপন রাখে।
এক্ষেত্রে নিজেরও কিছুটা দ্রুত বুদ্ধি খাটাতে হবে। তবে এই খেলাটি যোগ করার চেয়ে কঠিন কিছু না, তবে আপনাকেঅবশ্যই দ্রুত ও নির্ভূল হতে হবে।
Leave a Reply
GIPHY App Key not set. Please check settings
#13
২ যার মন পড়তে চাচ্ছেন তাকে পর পর ৩ টি ধনাত্মক ক্রমিক সংখ্যা লিখতে বলুন। এগুলি যে কোন পূর্ণ সংখ্যা হতে পারে তবে অবশ্যই এদের ক্রমিক সংখ্যা হতে হবে। (এদের মধ্যে কোনও পূর্ণ সংখ্যা থাকতে পারে না))
উদাহরণস্বরূপ, তিনি ১৯,২০ এবং ২১ বাছাই করতে পারেন।
যদি ক্যালকুলেটরের কেবল আট ডিজিট প্রদর্শনের জন্য ঘর থাকে, তবে সংখ্যাগুলো অবশ্যই ১ এবং ২১ এর মধ্যে হতে হবে। যদি ক্যালকুলেটরে কেবল ছয়টি ডিজিট প্রদর্শনের জন্য ঘর থাকে তবে এটি ১থেকে ৯ এর মধ্যে নির্বাচন করতে বলুন।
Leave a Reply
GIPHY App Key not set. Please check settings
#14
#15
৪ আরও তিনটি ক্রমিক সংখ্যার জন্য এই কৌশল পুনরাবৃত্তি করতে বলুন। এরপরে, আপনি যার মন পড়তে চাইছেন তাকে আরও তিনটি ক্রমিক সংখ্যা নিতে বলুন। তিনি সেগুলোকে আবার একসাথে গুন করবেন এবং তাদের প্রথম উত্তরের পাশে লিখে রাখবেন।
ধরা যাক তিনি ১২,১৩,১৪ বাছাই করেছেন। তিনি পেলেন ১২ x ১৩ x ১৪= ২১৮৪।
৫ তাকে দুটি উত্তর একসাথে গুণ করতে বলুন। এখন তিনি তার দুটি উত্তর একসাথে গুণ করে ফলাফল লিখেছেন।
৭৯৮০ x ২১৮৪ = ১৭৪২৮৩২০।
Leave a Reply
GIPHY App Key not set. Please check settings
#16
৬ যার মন পড়ছেন তাকে বলুন একটি অঙ্ক বাদে বাকিগুলো পরিবর্তন করতে। তাকে বলুন করুন যে সে কেবলমাত্র তাঁর মন থেকে আপনি একটিমাত্র অঙ্ক পড়তে পারবেন। তাকে সংখ্যাটি থেকে একটিমাত্র গোপন অঙ্ক বেছে নিতে বলুন, তারপরে অন্য অঙ্কগুলি যে কোনও ক্রমে বদলে দেওয়ার পরে লিখতে বলুন।
উদাহরণস্বরূপ, যদি তিনি ৪ অংকটিকে গোপন অঙ্ক হিসাবে বেছে নেন, তবে তিনি বাকি অঙ্কগুলি ২২৮৭০১৩ হিসাবে বদলে দিতে পারেন।
Leave a Reply
GIPHY App Key not set. Please check settings
#17
তাকে বাকি অংকগুলো জোরে জোরে পড়তে পড়তে বলুন এবং যোগ করুন। তাকে আবারও মনে করিয়ে দিন যে তাকে অবশ্যই একটি ডিজিট গোপন রাখতে হবে। এখন আপনি তাকে অন্য অঙ্কগুলি ধীরে ধীরে এবং পরিষ্কারভাবে পড়তে বলুন আর আপনি সেগুলি আপনার মাথায় যোগ করতে থাকুন।
উদাহরণস্বরূপ, তিনি "২ ... ২ ... ৮... ৭ ... ০ ... ১ ... ৩." পড়লেন। তিনি পড়ে যাওয়ার সাথে সাথে আপনি এগুলি যোগ করে মোট ২৩ পেলেন।
Leave a Reply
GIPHY App Key not set. Please check settings
#18
৮ গোপন অঙ্কটি খুঁজে বের করুন। গোপন অংকটি সহ তার উত্তরের সমস্ত অঙ্ক ৯ এর গুনিতক হবে। তাই এখন গোপন অঙ্কটি খুঁজে বের করার দুটি উপায় রয়েছে। উপায়গুলো হলোঃ
আমাদের উদাহরণে:
জানা অংকগুলি যোগ করলে ২৩ হয় এবং আপনি জানেন ৯ এর পরবর্তী গুনিতকটি ২৭। এখন ২৭ -২৩ = ৪ হয়, সুতরাং অংকটি ৪ হবে।
আপনি যদি ৯ এর পরবর্তী গুণিতকটি না জানেন তবে আপনার যোগফলের অঙ্কগুলি যোগ করুন এবং পুনরাবৃত্তি করুন। উদাহরণস্বরূপ, ২৩ → ২+৩ = ৫. এখন ৯ এর পরবর্তী গুণিতকটি ৯ , এবং ৯-৫=৪।
Leave a Reply
GIPHY App Key not set. Please check settings
#19
জানা অংকগুলোর যোগফল যদি ৯ পর্যন্ত হয় কি করতে হবে তা জানুন। অংকগুলো উচ্চস্বরে উচ্চারণ করার সময় আপনার যোগফল ইতিমধ্যে যদি ৯ এর অধিক হয়, তার অর্থ হলো দুটি সম্ভাবনা রয়েছে। হয় গোপন অংকটি ০ বা গোপন অংকটি ৯।এখন যেকোনো একটি অনুমান করুন। যদি আপনি এটি ভুল হয়ে থাকেন তবে একটু মজা করুন ("আমি জানতাম আমার টেলিপ্যাথি স্কুলে আরও বেশি পড়াশোনা করা উচিত ছিল"), এবার দ্বিতীয় সম্ভাবনাটি নিয়ে আবার অনুমান করুন।
Leave a Reply
GIPHY App Key not set. Please check settings
#20
আসুন জেনে নিই কেন এটি কাজ করে। যে কোনও তিনটি ধারাবাহিক সংখ্যায় ৩ এর গুণিতক থাকে, সুতরাং ত্রয়ীর গুণফলে ৩ এর গুণক হবে। যেহেত এটি পুনরাবৃত্তি করা হলো এবং দুটি উত্তর একসাথে গুণ করা হলো, আপনি প্রতিবার ৩ এর বর্গেরগুণমান পেয়ে যাচ্ছেন। অর্থাৎ এই উত্তরটি সর্বদা ৯(৩ x৩ = ৯ থেকে) এর গুনিতক। ৯ এর সমস্ত গুণিতকের উপরের কৌশলটি কাজ করবে।
Leave a Reply
GIPHY App Key not set. Please check settings
This post was created with our nice and easy submission form. Create your post!


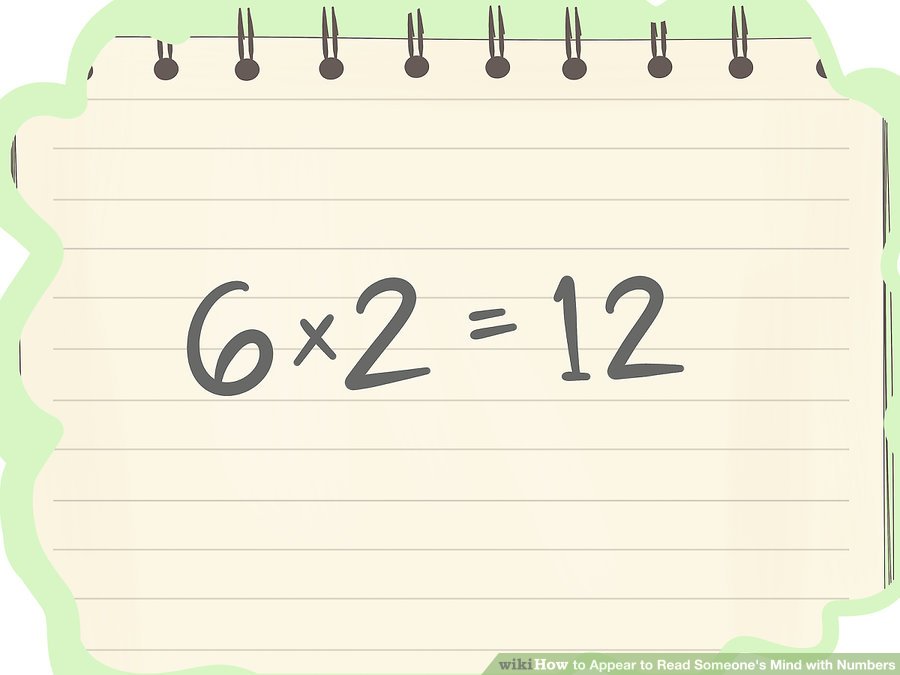
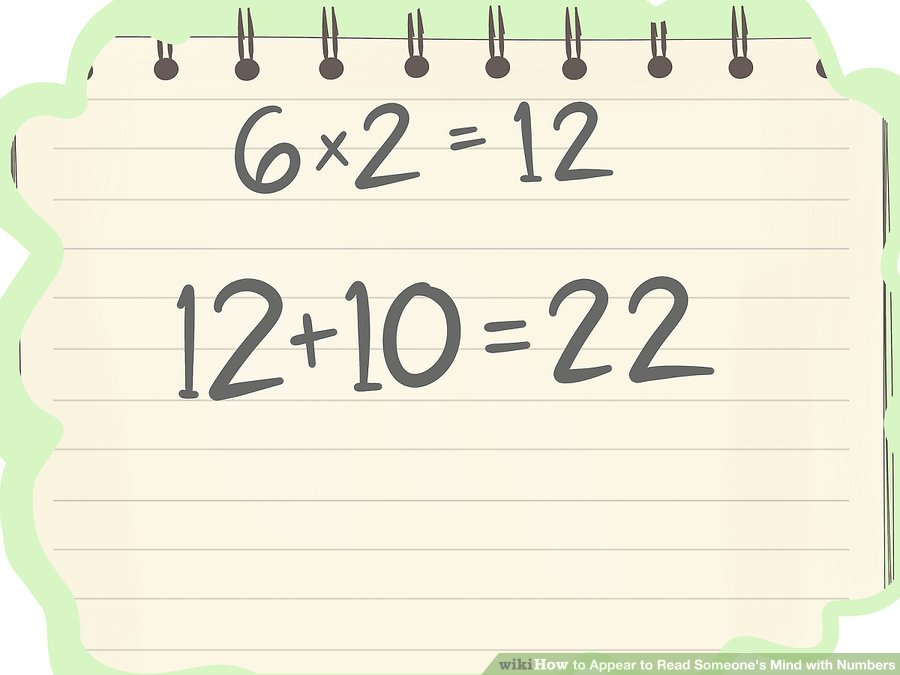
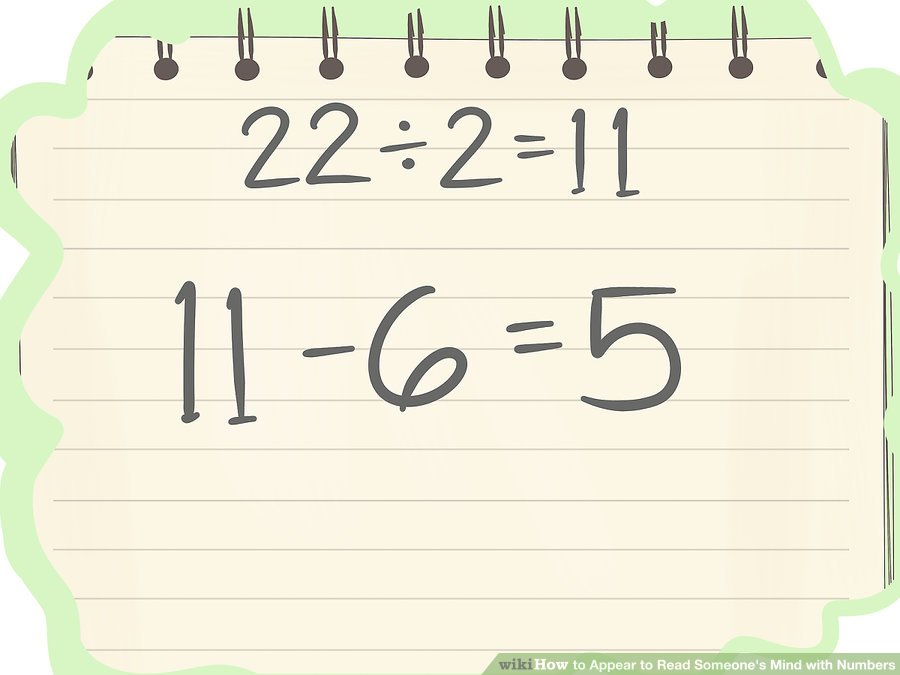

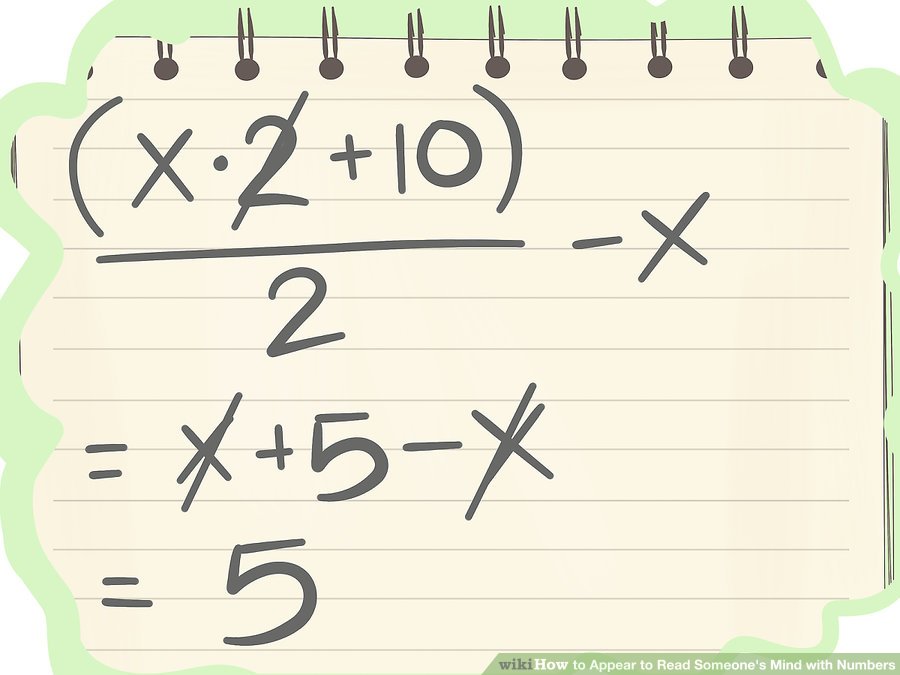

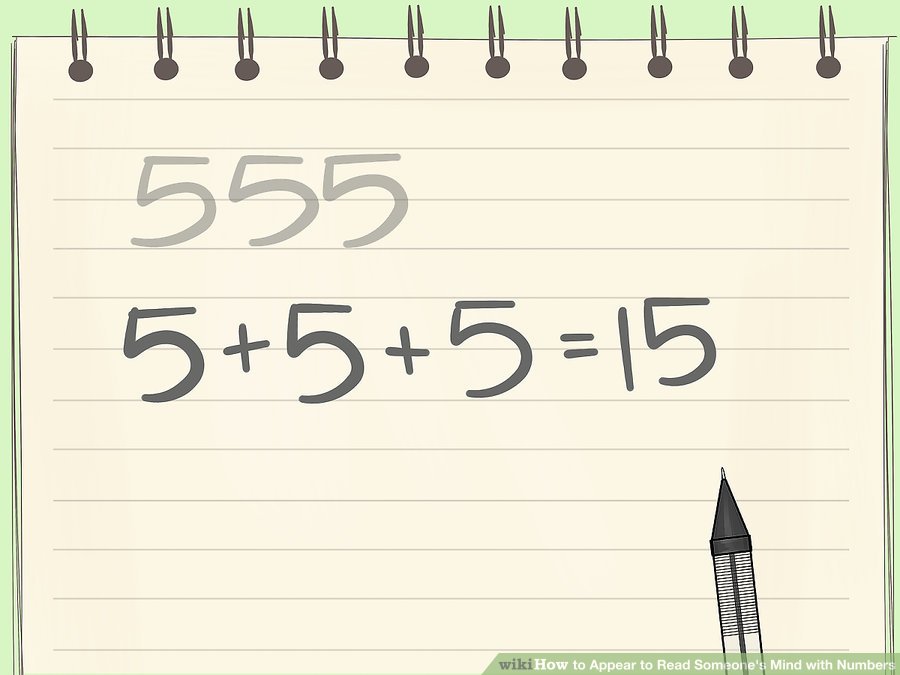


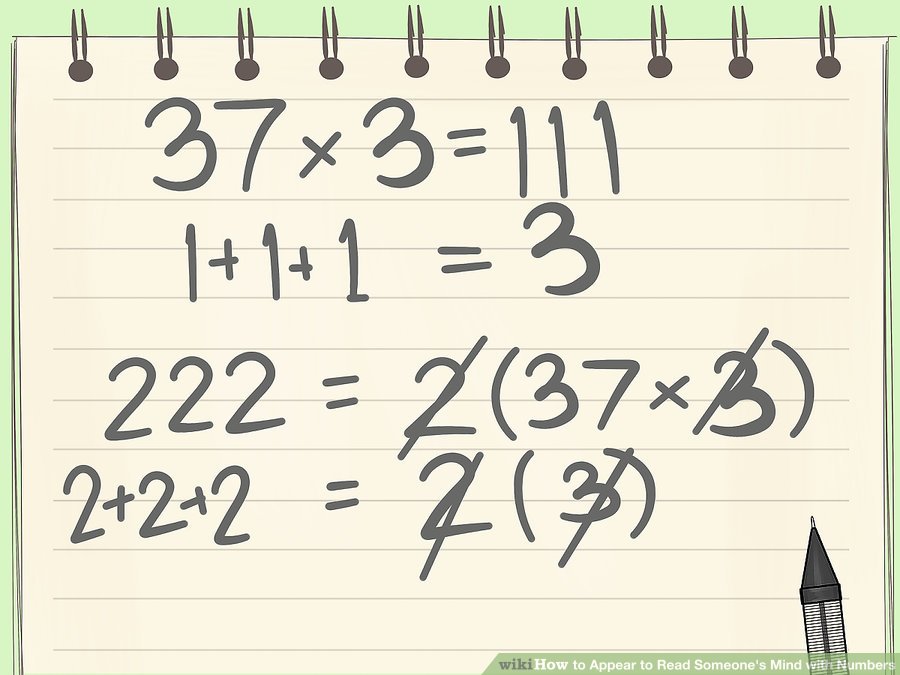


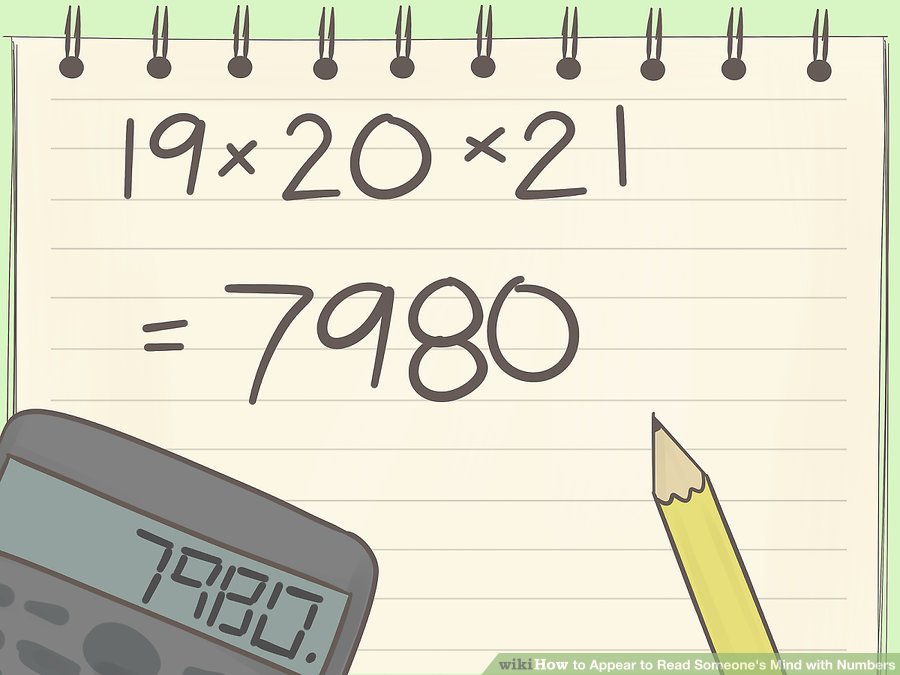
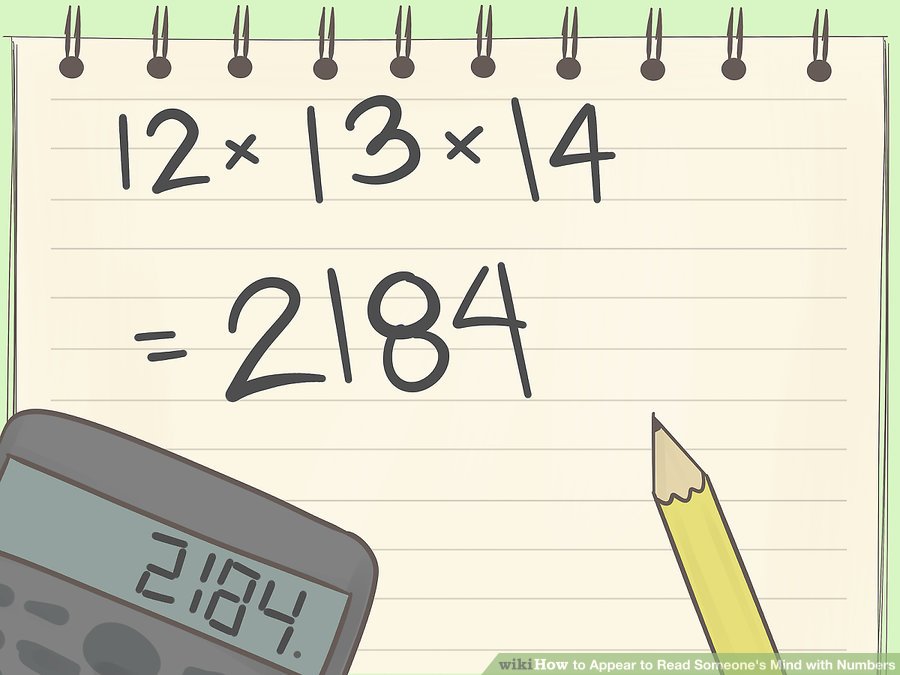

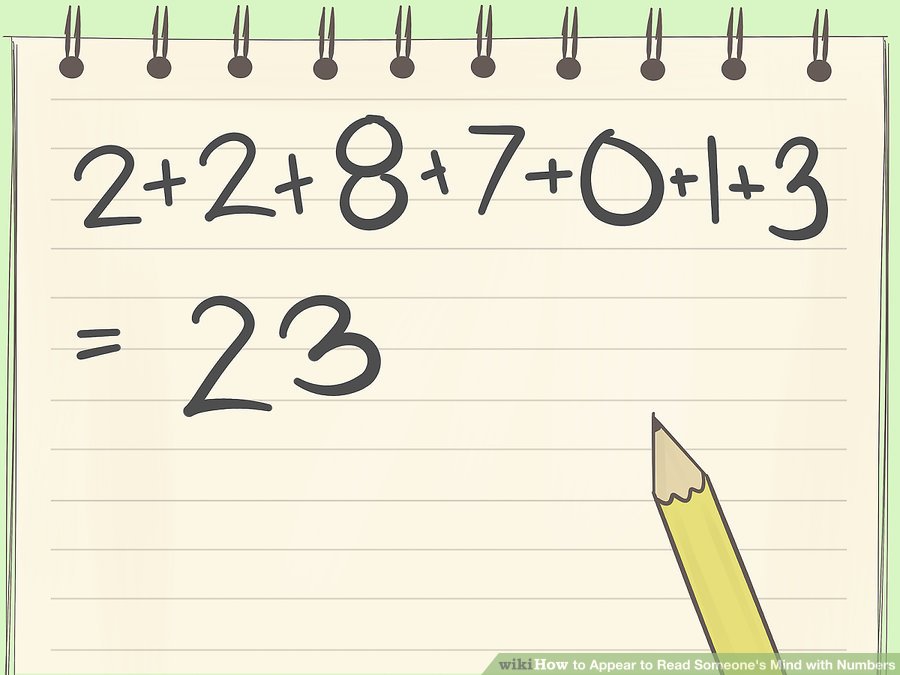

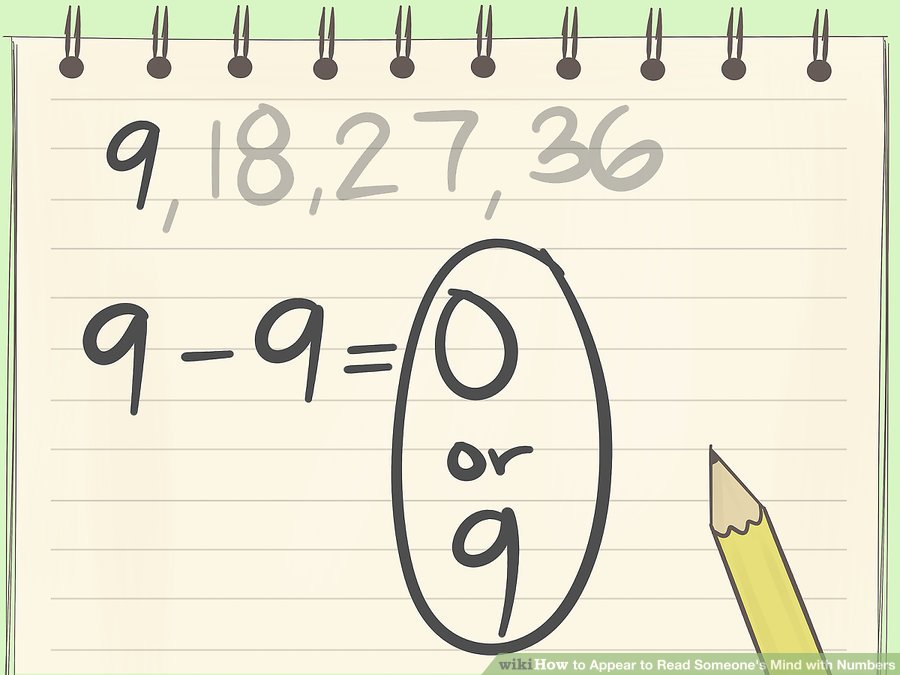
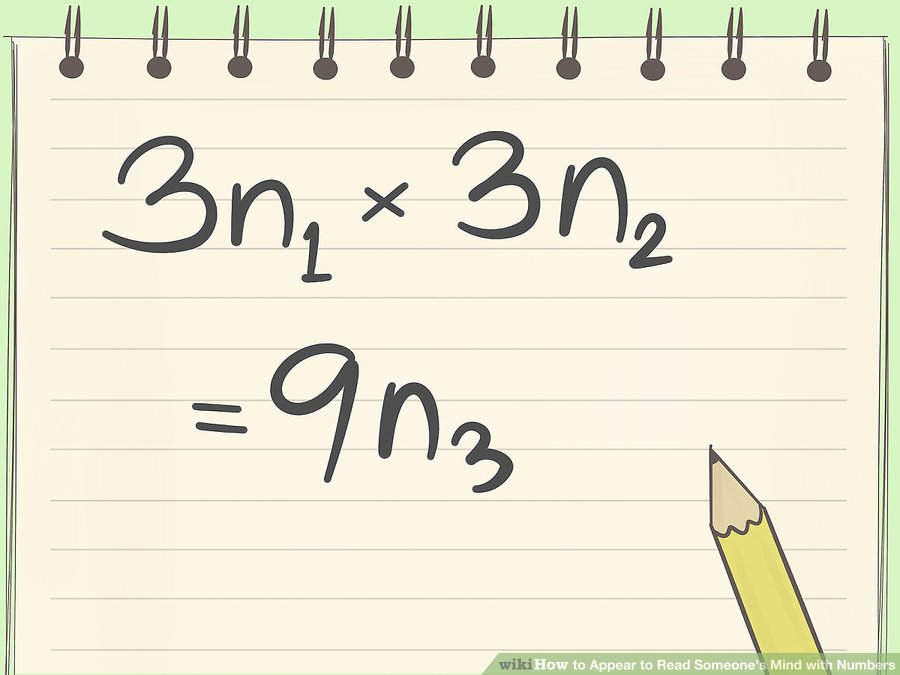



GIPHY App Key not set. Please check settings